 На
главную страницу
| Мои
темы
На
главную страницу
| Мои
темы На
главную страницу
| Мои
темы
На
главную страницу
| Мои
темы![]()
Жук на конвейере
Итак, предложена
задача: Жук на гусенице танка. Гусеница длиной L состоит из n секций (звеньев).
Танк перевернут и неподвижен относительно земли. Гусеница движется с релятивистской
скоростью – V=0.99 C. На гусенице сидит Жук. Вопрос: сколько звеньев видит
жук на гусенице (на своей и на противоположной стороне)?
Лобовое решение таково: с точки зрения Жука расстояние между ведущими осями
транспортера (гусеницы) сокращается в G раз. Значит, Жук на своей стороне
видит в G раз меньше секций. Например, если всего секций в гусинице 40, жук
на своей стороне видит
N1=((L)/G)/(L/2n) = ~2.8
секций вместо двадцати.. С этим еще можно было бы примириться, однако вопрос:
а где остальные секции гусеницы? Может быть, на другой стороне? Проверим это.
Для Жука скорость второй гусеницы составляет уже V’ =0.999949498 С. Для такой
скорости G1=99.503005! И количество секций –
N1=((L)/G)/(L/( G1*2n)) =~280!
Откуда лишние секции? Парадокс, однако...
Нет, тут явно что-то не так. Как поступим? А применим-ка метод, который уже
применялся в анализе парадокса близнецов.
Но сначала несколько важных идеализаций.
1. Гусеница представляет собой бесконечно тонкую бесконечно гибкую
ленту (типа транспортерной, но идеальную).
2. Валы, направляющие движение ленты, имеют пренебрежимо малый диаметр.
3. Секции гусеницы представляют собой просто разметку на ленте транспортеоа,
нарисованы на ней.
4. К моменту начала рассмотрения задачи все скорости считаем установившимися.
Таким образом, считаем, что движение элементов ленты осуществляется ПО ОДНОЙ
линии: вперед и назад (что, однако, не создают помех для элементов на встречных
направлениях).
Итак, для
начала возьмем Жука и жука-близнеца, и посадим их на противоположные секции
гусеницы. Оснастим жуков генераторами с единичной частотой, приемниками, и
пожелаем им удачи...
Зададимся длиной гусеницы – L=C (для простоты). Зададимся скоростью гусеницы
V=0.99*C. Дадим жукам передатчики с частотой f0=1. (кто хочет – считайте в
мега- или гигагерцах). Воспользуемся данными из решенной ранее задачки о близнецах
(в части «Симметричный полет»):
f1=199.00099*f0;
f2=0.0050251*f0;
Рассмотрим сначала из ИСО, связанной с центрами валов, какие события происходят
с жуками на очередном витке. Витки начинаем с положения, когда жуки максимально
удалены (Рис. 1).
1.
Старт жука .
2. Встреча фронта сигнала от приближающегося близнеца.
3. Встреча самого близнеца.
4. Финиш.
Между событиями
1-4 пройдет t=L/C=1/0.99=1.01010101 c
Между событиями 1-2 пройдет время, которое находим из уравнения:
t1*(V+C)=L; t1=1/1.99=0.50251256 c.
Между событиями 3-4 пройдет время t3=0.505050505 c, т.к. встреча произойдет
ровно на середине пути. Между событиями 2-3 пройдкт время t2=t-t1-t3=0.00253795
c.
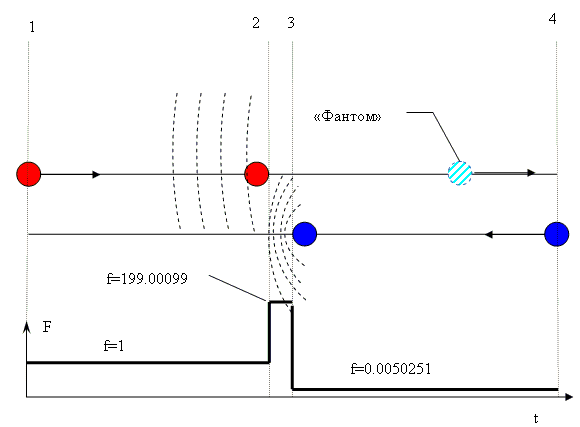
Рис. 1.
Встрчный полет.
От исходного положения – 1 Жук (красный кружок) принимает радиосигнал
от близнеца когда тот уже движется навстречу – видит «фантома». В положении
2 Жук встречает фронт волны, несущей инфориацию о старте близнеца, и после
точки 3 принимает пониженную Допплером частоту.
Теперь перейдем
в ИСО первого Жука. Его время течет замедленно (известно, во сколько раз).
Но теперь это не существенно. Важно, что и в ИСО жука события 1...4 делят
время между стартом и финишем в том же отношении. Т.е:
t’:t’1:t’2:t’3=1.010101010:0.50251256: 0.00253795: 0.505050505.
Прежде, чем заняться подсчетом импульсов, принимаемых Жуком от близнеца, хочу
обратить внимание на принципиальный момент: может показаться, что на участке
1-2 Жук не принимает радиосигналов до момента, пока не встретит фронт радиоизлучения
от приближающегося близнеца. Но это не так. На самом деле он сразу после поворота
начинает принимать радиосигналы от близнеца, испущенные до ЕГО поворота, т.е.
когда тот еще двигался В ТУ ЖЕ СТОРОНУ, что и Жук теперь. То есть, они как
бы находятся в одной ИСО. И частота приема равна 1. На участке 2-3 принимается
частота повышенная Допплер-эффектом. На участке 3-4 – пониженная. Итак:
N1=t’1*f0=(t/G)*0.50251256*1;
N2=t’2*f1=(t/G)*0.00253794*199.00099;
N3=t’3*f2=(t/G)*0505050505*0.0050251;
N=N1+N2+N3=(t/G)*( 0.50251256+0.505053904+0.00253793)= (t/G)*1.010101 ;
Иными словами, Жук за один проход от «старта» до «финиша», т.е от момента,
что перевалил на «верхнюю» сторону гусиницы и до следующего отражения, Жук
принял от близнеца ровно столько же периодов, сколько испустил его собственный
передатчик. И, что очень важно, принял ВСЕ периоды от близнеца за ЕГО цикл.
Отсюда - некоторые выводы:
1.
У обоих жуков время идет в одинаковом темпе.
2. Жуки встречаются ровно посредине гусеницы.
3. Темп времени обоих жуков замедлен в G раз.
Но главный
интерес сейчас представляет график принимаемой Жуком частоты (Рис 1). Рассмотрим
его и заметим такие интересные вещи: Жук почти пол дороги «видит» своего близнеца,
«едущего» впереди в том же направлении с той же скоростью. Объясняется это
тем, что Жук продолжает принимать радиосигналы, «оставленные» близнецом на
предыдущем витке и продолжающие даижение уже тогда, когда сам близнец движется
назад... Затем следует резкий короткий всплеск частоты – разворот близнеца.
В это время Жук «видит» его приближение, а затем частота так же резко уменьшается
– близнец удаляется...
Мне могут возразить, что жук на самом деле видит фантома, ведь близнец почти
все время «ехал» навстречу на другой стороне гусеницы... А как наш Жук может
узнать, фантом это, или нет? Увы, нет такого способа... Точно так же, мы,
разглядывая удаленную звезду, не знаем, не фантом ли это...
Ну а теперь осталось пригласить еще несколько жуков-помощников, оснастить
их передатчиками, рассадить по всем секциям гусеницы и построить такой же
график частоты, принимаемой от КАЖДОГО жука...
Конечно, построить 39 дополнительных графиков – довольно трудоемкое дело.
Поэтому я позволил себе сократить количество секций и жуков до 6. На рис.
2, а схематично изображены основные фазы прцесса движения гусеницы. При этом
жуки изображены кружками разного цвета.
А на рис. 2, б изображены графики частот, принимаемых Жуком ( красный кружок)
от всех участников движения (напоминаю, что частоты и длительности не выдержаны
строго в масштабе).
Удивительные вещи открываются при анализе этих графиков.
Итак, сразу после поворота на очередную сторону Жук видит... ВСЕ ОСТАЛЬНЫЕ
СЕКЦИИ (точнее, сидящих на на них жуков-помощников) одновременно! Затем самая
дальняя секция как бы «проваливается», исчезает из поля зрения (переходит
на «встречную полосу»), после чего следует короткая вспышка высокочастотного
сигнала (так видится встречное движение), и сразу после этого – низкочастотный
сигнал (так видится взаимное удаление). Жук видит 4-х товарищей, едущих вместе
с ним по его стороне гусиницы и одного – удаляющегося по другой стороне...
Затем «проваливается» следующая секция и т.д ...То же последовательно повторяется
с каждым едущим впереди жуком-помощником.
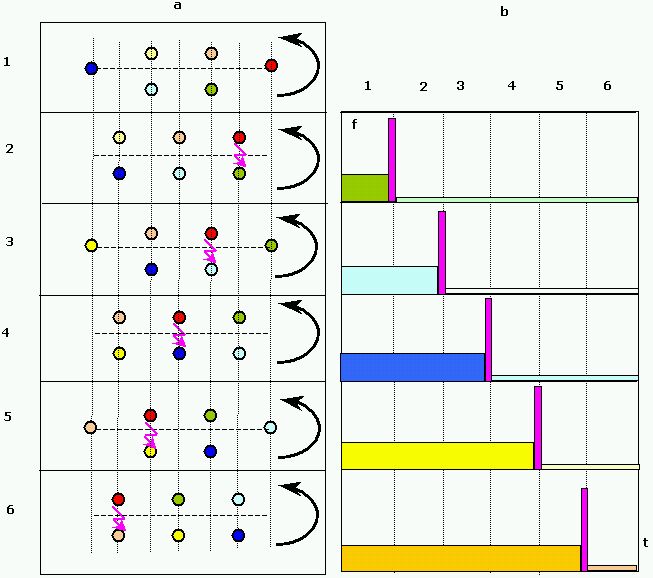
Рис 2.
Фазы движения
а – фазы движения транспортера с 6-ю жуками.
б – графиеи приема частот от каждого из жуков.
В фазе 1 Жук видит ВСЕХ своих партнеров, едущими впереди с той же скоростью
В фазе 6 Жук видит вех своих партнеров движущимися по другой стороне транспортера.
Частоты, получаемые от каждого из жуков, помечены соответствующим цветом,
Фиолетовым цветом помечены частоты, повыщенные Допплером при встречном движении.
Частоты пониженные Допплером при расхождении, помечены менее насыщенными цветами..
После исчезновения
последнего Жук видит себя ОДНОГО стоящего на своей секции и 5 удаляющихся
по другой стороне помощников. Ну а в следующий момент Жук сам переваливается
через загиб транспортера – и в следующее мгновение он видит впереди себя всех
помощников... Все повторяется сначала...
Остается добавить, что что для заданной скорости качественно картина не изменится
и для 40 секций на гусинеце...