 На
главную страницу
| Мои
темы
На
главную страницу
| Мои
темы На
главную страницу
| Мои
темы
На
главную страницу
| Мои
темы![]()
Черная Луна
или
Измерение скорости грвитации
Согласно
ОТО, гравитационное взаимодействие распространяется со скоростью света. С
другой стороны, до настоящего времени нет надежных эксперементальных фактов,
подтверждающих это. Правда, в последнее время появились сообщения об ИЗМЕРЕНИЯХ
скорости гравитационного взаимодействия (http://grani.ru/Society/Science/m.18983.html).
Там в целом подтверждается равенство скорости распространения гравитационного
взаимодействия скорости света. Но почему-то у многих преобладают скептические
отношения к приведенным результатам. Что же касается альтернативщиков всех
мастей, они предпочитают говорить об иных скоростях распространения гравитации
- от бесконечной, до удвоенной световой.
Существуют ли иные, относительно простые способы измерения скорости гравитационного
взаимодействия? На мой взгляд - хотя бы один такой способ существует. Этот
способ я предложил много лет назад, однако по ряду причин, сам поставить эксперимент
не смог. Мне не удалось убедить дирекцию организации, в которой я работал,
и которая занималась проблемами иного рода, создать для этого что-то вроде
лаборатории. Прблема заключалась в помещении - оно должно быть глубоко под
землей, чтобы защитить измерительные приборы от температурных и прочих помех...
Вероятно, я не был достаточно настойчив, а потом другие заботы и проблемы
заставили меня забыть об этой затее... Публикации вроде упомянутой напомнили
мне о старой идее...
Суть идеи проста. Известно, что свет от Солнца доходит до Земли за время порядка
8,5 мин. На первый взгдяд может показаться, что в момент, например, восхода,
Солнце "на самом деле" находится уже гораздо выше над линией горизонта.
И если бы существовала возможность видеть "гравитационное" Солнце,
могло бы оказаться, что положение "гравитационного", (назовем его
черным) Солнца не совпадает с его видимым положением. Это дало бы возможность
оценить отношение скорости распространения гравитационного взаимодействия
к скорости света. Именно такова была идея в своем исходном виде... Но к сожалению,
Солнце для этой цели не подходит. Не вдаваясь в подробности, отмечу только,
что положения черного и обычного, видимого Солнца совпадают вне зависимости
от соотношения скоростей света и гравитации. Когда я это понял, это было для
меня сильным разочарованием! На самом деле некоторые расхождения между видимым
положением Солнца и его “черным” двойником может быть. Но мы ограничимся рассмотрением
другой возможности.
Существует еще и Луна. И именно Луна может дать возможность измерить скорость
гравитации. Положение на небосводе «черной», гравитационной Луны может и не
совпадать с ее видимым положением. Разница во времени может составить все
те же 1.3 с, (время, которое свет затрачивает на путь Луна – Земля), или расхождение
примерно на 1/100 видимого поперечника Луны, если гравитация распространяется
мгновенно. Вполне солидная величина и поэтому имеет смысл за ней поохотиться...
Замечу, что возможное расхождение черной и видимой Лун обусловлено не суточным
вращением Земли, а орбитальным движением Луны. Это, однако, может иметь значение
только в случае, если будет зафиксировано несовпадение полложений на небосклоне
«черной» и видимой Лун – для анализа скорости гравитации – превышает ли она
световую, или меньше ее?

Рис. 1
Приливные явления – гравитационные искажение сферической формы Земли.
Рисунок заимствован на сайте http://230nsc1.phy-astr.gsu.edu/hbase/hframe.html
Как, однако увидеть «черную», гравитационную Луну? На мой взгляд, если и не
увидеть, то определить НАПРАВЛЕНИЕ на нее достаточно просто. На нее указывает
вектор градиента напряженности гравитационного поля! Или, что то же самое, вектор
приливных ускорений (или сил). Мы знаем, что приливные силы деформируют Землю
- она вытягивается, причем направление "вытягивания" как раз указывает
на гравитационную, "черную" Луну (Рис. 1.) Существуют также и приливные
силы от Солнца, но о них позднее. Конечно, по деформации Земли определить направление
затруднительно. Известно, однако, что приливной «горб» определяет направление,
составляющее с направлением на видимую Луну 3 угловых градуса. Но никто и не
заставляет определять направление по этому «горбу». Вместо этого можно просто
точно измерять значение ускорения свободного падения или вес пробного грузика
в некой точке... Что собой должен представлять график изменения веса за сутки?
В самом первом приближении, это должен быть график функции вида
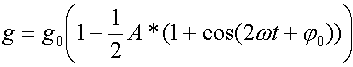 (1)
(1)
Здесь
А – некая константа, характеризующая размах колебаний значений ускорения свободного
падения (оценка приводится ниже), вызванных влиянием приливных ускорений, -
круговая частота, соответствующая периоду в одни сутки.
За сутки указанная функция должна дважды принимать минимальнье значение, соответствующее
максимуму приливных сил. Один из этих экстремумов соответствуют наивысшему положению
Луны на небосводе. И вот именно тут есть возможность проверить, как соотносятся
между собой время экстремума значения ускорения, и момента нахождения Луны в
наивысшеи положении. Тоесть, совпадает ли видимое положение на небосклоне «черной»
и обычной Лун? Ну а дальше – дело техники: если момент экстремума g совпадает
по времени с моментом наивысшего положения видимой Луны - скорость распространения
гравитации равна скорости света. Если будет зафиксировано несовпадение - это
даст возможность оценить скорость гравитации (Рис. 2)...
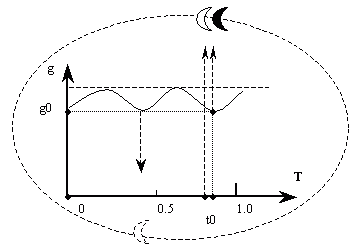
Рис.
2.
Измерение скорости распространения гравитации сводится к определению времени
максимального приливного ускорения и сравнения этого времени с временем
максимально высокого положения видимой Луны...
Конечно,
в реальной жизни для выполнения таких измерений необходимо решить не одну проблему.
Главное, кроме обеспечения защиты от всех «обычных» помех, необходимо учесть
и исключить погрешность, вызываемую влиянием солнечных приливных ускорений,
которые составляют до 44% от лунных. Это можно осуществить при обработке данных,
тщательно расчитав теоретически и вычтя вклад солнечных приливных сил. Можно
подобрать оптимальное значение фазы Луны - наилучшее состояние, на мой взгляд,
это ново - или полнолуние. Идеально подходит момент полного солненчного затмения
– эти моменты характеризуются минимом фазовой погрешности от влияния солнечных
приливных ускорений. Необходимо добиться чрезвычайно высокой точности измерений.
Так, относительное изменение g (параметр А), связанное с приливными силами,
составляет величину порядка (2*Е-7). Для того, чтобы зарегистрировать время
максимума с точностью до десятых долей секунды, необходимо повысить чувствительность
еще на 4 - 5 порядков! Это уже вырастает в серьезнейшую проблему. Например,
если представить себе пружину, растянутую грузиком на 20 м, необходимо регистрировать
изменение ее длины в диапзоне +-(4 – 6 ) мкм. С разрешением не хуже 0.5 – 0.1
нм. Тоесть, чувствительность измерений должна соответствоавть размерам атомов...
В принципе это возможно, хотя и достаточно сложно. Впрочем, это – лобовое решение.
Уверен, что на сегодняшний день существуют более чувствительные и точные методики.
Необходимо... Да много чего еще необходимо! Но главное - идея, думаю, ясна.
И, на мой взгляд, вполне осуществима. Возможно, даже нет необходимости в создании
специальной аппаратуры, детекторов, методик и т.д. Измерения, вероятно, могут
быть выполнены на многих из существующих астрономических обсерваторий. Более
сложный, но, вероятно, тоже осуществимый способ - наблюдение за возмущением
орбит ИСЗ и т. д...
Приглашаю обсудить вопрос: осуществимо ли подобное измерение? Кто возьмется
практически воплотить его в жизнь? Ставка может быть достаточно высока: мировая
известность, вроде той, что пришла к Копейкину...