Парадокс близнецов

Разбор полетов в числах

    1. Классический парадокс близнецов

      Давайте попробуем внести ясность в вопрос о т.н. "парадоксе близнецов".  Итак, имеется: два близнеца, один из которых спокойно сидит дома (назовем его «Неподвижный»), другой (назовем его «Летящий») отправляется на Чудо-ракете в космос. Почему чудо-ракета? А потому, что она можкт мгновенно разгоняться до околосветовой скорости и так же мгновенно может менять направление полета. Это в жизни невозможно, зато гораздо легче просчитывается, поэтому игра стоит свеч, да и не так это важно, надеюсь, это станет ясно далее. А мы зададимся конкретными условиями и все выкладки проведем не в общем виде, а , для большей наглядности, в численном.
     Итак, Неподвижный сидит себе дома, а Летящий выстреливается в космос со скоростью 0.99*С. Ему предстоит пролететь расстояние L=1000000*C, мгновенно развернуться и с той же скоростью вернуться назад. Близнецы в своем принципиальном споре решили ничего не принимать на веру, а вместо этого -  непосредственно контролировать течение времени друг у друга.  Для этого они берут 2 идентичных генератора, один устанавливают в ракете, а другой - дома у оставшегося близнеца. Эти генераторы подсоеденены к передатчикам, которые включаются во время старта и все время излучают электромагнитную волну, и каждый из бизнецов все время принимает сигнал от другого. Время отсчитывается в периодах генератора (для обладающих раскованной фантазией можем использовать удары сердца, или упаковка мешочков, или что-либо еще). Для простоты частоту генераторов возьмем f=1Гц.  Итак, разбор полета -

    а). С позиции Неподвижного.

Для неподвижного близнеца между стартом и возвращением ракеты пройдет время
T=2L/V=2020202 c., или в периодах генератора
N=T*f=2020202.
Что будет наблюдать Летящий после старта? Ну, прежде всего он заметит, что частота принимаегмого от сигнала от Неподвижного низкая: в полном соответствии с эффектом Доплера. Зато после разворота частота сигнала резко возрастает (по той же причине). В формулу эффекта Допплера входят 2 сомножителя. Один из них описывает классический  Допплер эффект, второй учитывает уменьшение темпа времени у объекта, имеющего некую скорсть относительно приемника. В этой части задачи Летящий считает периоды, не сильно обращая внимание на частоту: ведь именно число периодов определяет время, которое течет у оставшегося близнеца. Сколько же периодов насчитает наш близнец? А ровно столько, сколько унеслось "волн " от генератора Неподвижного за время, что Летящий провел в полете. Пусть в разном темпе на разных участках пути, но он примет (почувствует!) каждую волну, распространяющуюся от генератора оставшегося близнеца.. И будет их, естественно, 2020202 (более подробный анализ – ниже). Тоесть, летящий близнец правильно определит время, прошедшее у оставщегося дома близнеца.
Теперь попробуем разобраться со временем Летящего. Для этого посмотрим, что насчитает Неподвижный, принимая радиосигнал от Летящего .
Прежде всего, Неподвижный тоже сначала увидит, что приходящий сигнал имеет более низкую частоту:
f1=f/G*(1+V/C)=1/(7.08881*(1+0.99))=0.070888 (Гц).

G=(1-V^2/C^2)^(-1/2)=7.08881.
Затем он увидит, что частота резко возросла:
f2=f/G*(1-V/C)=1/(7.08881*(1-0.99))=14.1 067 (Гц).
Чтобы сосчитать число периодов, необходимо еще знать время, в течении которого принимаются сигналы на этих частотах. И вот тут необходимо удержаться от грубой ошибки! Ведь то, что путешесчтвенник развернулся и двинулся назад, оставшийся близнец узнает не сразу: фронт сигнала, несущий информацию об изменении направления движения, должен сначала преодолеть расстояние от места, где близнец развернулся, до оставшегося близнеца! Назад "наперегонки " несутся сначала фронт волны, затем, отставая, сам Летящий! Первым придет, конечно, волновой фронт, а затем, через
T2=L(1/V-1/C)=10101.01 (с),
появится и сам Летящий - это и будет конец полета.
Остается найти время, в течении которого Неподвижный принимал сигнал с низкой частотой:
T1=T-t2=2L/V-L(1/V-1/C)=L(1/V+1/C)=2010101 (c).
Наконец, периодов в первом и втором случае будет подсчитано:
N1=T1*f1=2010101*0.070888 =142492;
N2=T2*f2=10101.01*14.1067 =142492;
Очень красиво, не правда ли?  Несмотря на то, что принимаемые частоты отличаются примерно в 200 раз, число принятых периодов, соответствующих участкам полета вперед и назад – одинаково. Поскольку часы Летящего отсчитали одинаковое время  при полете туда и обратно...

Ну и общее время, которое получит оставшийся близнец, составит 284984 периодов - а значит, в ракете за все время полета прошло всего 284984 секунды. Что в 2020202/284984=7.08881 - ровно в G раз меньше, чем прошло в системе оставшегося близнеца!
     Обращаю внимание, что задача по сути дела чисто кинематическая. Никаких эффектов ОТО привлекать не надо. Ускорения также не играют особой роли. Главное - изменение направления движения, которое ломает всю кажущуюся симметрию ситуации.

Давайте подведем предварительный итог полета.  Итак, с точки зрения  Неподвижного близнеца путешествие его брата должно занять 2020202с, или около 23 суток. После старта ракеты Неподвижный начинает принимать сигнал от Летящего на частоте f1=0.0708881Гц. По расчетам Неподвижного, через 1010101 с ракета должна достигнуть цели и повернуть обратно. Однако через 11.5 суток ничего не меняется: Неподвижный продолжает принимать сигнал на той же частоте f1! И так продолжается почти все расчетное время полета и лишь за 2.8 ч. до расчетного времени возвращения характер сигнала резко меняется: частота скачком (напоминаю о условностях) возрастает до величины f2=14.1067Гц. В итоге Неподвижный примет 124492 периода на низкой частоте и столько же - на высокой. Отсюда получается, что в ракете прошло 284984 с ( около 3.3 суток) , что ровно в G раз меньше, чем у Неподвижного.

     Тут я хочу опять остановиться на ключевом моменте: с ракетой произошло Событие - ракета изментла направление полета! Ракета в полете "туда " была в одной инерциальной системе отсчета, затем перешла в другую (через шок, ускорение, хотя это, я подчеркиваю, не принципиально!) и двинулась "обратно ". Поскольку Событие произошло с ракетой, когда она была удалена от земли, Неподвижный не мог узнать о нем ранее, чем световой сигнал с места события достиг земли. Именно этим объясняется столь разное время приема на низкой и высокой частотах... Кстати, Неподвижный определил, что в системе ракеты время движения вперед и назад одинаково (а иначе и быть не могло).

Продолжим разбор полета –

    б). С позиции Летящго.

    Вот теперь мы готовы к путешествию вместе с Летящим. После старта, придя в себя от легкого шока, вызванного бесконечным ускорением, Летящий убедится, что он принимает сигнал на частоте f1=0.0708881 Гц. Пока ситуация выглядит симметричной... Каждый из близнецов вправе считать, чо это у другого время течет медленнее... Если им не доведется больше встретиться, этот вопрос так никогда и не будет решен! Но будем надеяться на лучшее...
Сколько периодов принимаемой частоы насчитает Летящий на  участке удаления? Для ответа надо найти продолжительность полета Летящего "туда ". Никаких отклонений  хода своих часов Летящий конечно же, не фиксирует. Зато он видит,  что пространство, несущееся ему навстречу, "укоротилось " в G раз! Во всяком случае, до отметки, на которой следует развернуться, он добертся за гораздо меньшее время, чем L/V, а именно за 

T=1000000/(0.99*G)=142492.2(c).

 Знакомое число! Именно таким определил время полета Летящего в одну сторону Неподвижный...

     И здесь необходимо отметить следующее: Событие происходит не с Землей, а с ракетой. Поэтому Летящий, находящийся в ракете, "узнает " о нем мгновенно: ведь Событие происходит не где-то там, а здесь, с ним! Соответственно, сразу изменится частота принимаемого сигнала. Почему? Да потому, что волновой порядок, распространяющийся от передатчика Неподвижного, уже существует, он начал выстраиваться одновременно со стартом летящего и ОПЕРЕЖАЕТ его ракету. И если при полете «туда» Летящий пересчитывает «гребни» электромагнитных волн, бьющих в его корму с одной частотой, после поворота Летящий начнет персчитывать их (бьющих уже в лицо) с другой частотой...  И с этого же момента вся симметрия летит в тартарары... Летящий за время полета ОДИНАКОВОЕ время принимает сигналы как на пониженной, так и на повышенной эффектом Допплера частоте и это - коренное отличие в ситуации близнецов...
Теперь можно определить число принятых периодов:
N1=T*f1=142492.2*0.0708881=10101.01.
N2=T*f2=142492.2*14.1067=2010101.
А всего - 2020202 периода, что позволяет Летящему определить, что на Земле прошло тех же 23 суток! Таким образом, детальный анализ подтверждает вывод, сделанный выше, о том, что Летящий правильно определит время, прошедшее по часам Неподвижного.

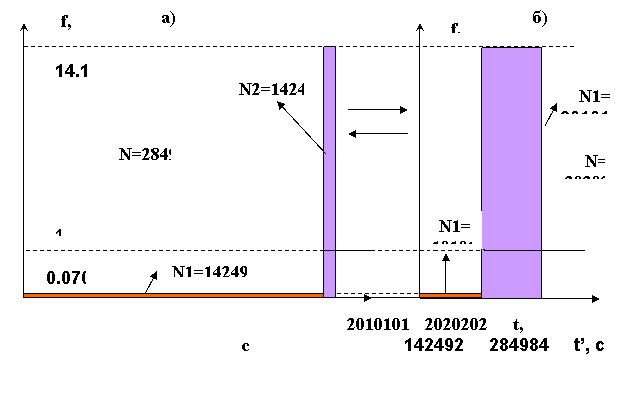
Рис. 1

Графики приема частот Неподвижным – а) и Летящим – б) близнецами.

Более наглядное представление о полете могут дать графики приема частот для каждого из близнецов.

...Давайте попробуем разобраться с близнецами из некоторых других схем полетов.

    2.  Близнец – невозвращенец

 Пусть с Земли стартует ракета, в которой Летящий улетает навсегда... Вопрос: у кого из близнезов время идет медленнее?
Для анализа возьмем данные из предыдущей задачи. Скорость - 0.99*С, расстояния теперь нет... Какие частоты принимают братья? Тут нет вопроса: и тот и другой принимают частоту 0.0708881Гц. Тоесть на каждый период, полученный от другого, собственный генератор делает 14.1067 периодов (если угодно - ударов сердца)! Понятно,  эффект Допплера. Но ситуация действительно кажется парадоксальной. А почему, собственно? Каждый близнец считает, что темп времени замедлился у другого, ну и что с того? Ведь они в разных инерциальных СО. Каждый из них, между прочим, показался бы другому укороченным!  А  с дальнего расстояния каждый к тому же выглядит очень маленьким... А что же «на самом деле»? Ответ, повидимому таков: нет никакого «на самом деле», пока близнецы находятся в разных инерциальных системах отсчета (СО).
     Чтобы проверить, что произошло на самом деле, НЕОБХОДИМО вернуться в одну СО. Как? А для этого необходимо сделать их взаимную скорость равной нулю. Тоесть, можно Летящему вернуться назад - этот вариант просчитан. Можно летящему просто остановиться. Чтобы увидеть, как изменится график частот, достаточно отбросить на Рис.1 участки, соответствующие приему высокой частоты (фиолетовый цвет) и заменить их на график f=1 (необходимо учесть, что маштабы на графике не выдержаны точно). И тогда окажется, что за время полета  (по условиям первой задачи) у неподвижного пройдет 2010101 с, а у летящего - 142492 с. О том, что Летящий остановился, неподвижный, естественно, узнает по изменившейся частоте приема.  И он споклйно констатирует: У летящего темп времени замедлен в 2010101/142492=14.1067 раз.

 Ну а что же Летящий? А он зафиксирует, что к моменту его остановки по его часам прошло 142492 с, а у Неподвижного – 10101с (ровно столько периодов частоты Летящий примет до своей остановки ). Значит, сделает он вывод, у Летящего темп времени замедлен в те же

142492/10101.01=14.1067 раз.

А вот это уже настоящий сюрприз! Оба близнеца и после остановки Летящего зафиксируют замедление времени друг у друга... Правда, у них будут разногласия по вопросу: сколько же времени прошло у Неподвижного до момента остановки Летящего. Но  это не так уж странно –  близнкцы находились в разных СО, а после остановки оказались в одной СО, но в отдаленных точках пространства. Впрочем, вопрос может быть решен, если подготовить заранее  синхронизированные  по определенным правилам часы. Тоесть, необходимо учитывать задержку в распространении радиосигнала... Ну а нам теперь понятно, где корень асимметрии близнецов:  Летящий узнал о своей остановке сразу, а Неподвижный - только после прихода фронта волны с измененной частотой ( в этом варианте задачи - 1 Гц).

   Наконец,  можно посадить Неподвижного в другую ракету и отправить вслед за Летящим! Но я не хочу злоупотреблять терпением читателя и предоставляю желающим возможность самостоятельно проанализировать этот вариант.

    3.  Двое Летящих (сммметричный полет)

   Наконец,  рассмотрим такой вариант: две ракеты стартуют в противоположные стороны, пролетают некоторое расстояние, разворачиваются и возвращаются в исходную точку. Вопрос: какова общая длительность полета каждого из близнецов, определенная ДРУГИМ близнецом?
Исходные данные берем из первой задачи: ракеты разлетаются на 1000000С км в обе стороны от Земли со скоростью 0.99С. Ускорение и разворот осуществляются мгновенно.

   Решение можно получить чрезвычайно просто: действительно, из предыдущей задачи мы знаем, что в ракете летящего проходит 284984 с времени, столько же периодов передает его генератор. Второй близнец, все время находящийся в волновом порядке генератора первого, "почувствует " каждый из этих периодов (не важно, какова частота приема на разных участках полета!). Значит, он правильно определит время полета первого. Аналогичный ответ получается и для первого близнеца. Но вот детальный анализ событий с точки зрения одного из близнецов будет несколько сложнее, и в нем присутствует новый элемент, поэтому такой анализ представляет самостоятельный интерес.
Итак, из точки О в противоположные стороны вылетают две ракеты А и Б. Анализ проведем для ракеты А, стартующей условно на восток. (Для второй получится то же самое - симметрия полная). Определим взаимную скорость ракет:
V'=(V+V)/(1+V^2/C^2)=1.98/(1+0.99^2) = 0.999949498 C ;

 для этой скорости

G'=(1-V'^2/C^2)^-1/2=99.503005;
Определим частоты, которые принимает ракета А при разлете:
f1=f/(G'*(1+V'/C)=0.0050251(Гц);
и при сближении:
f2=f/(G'*(1-V'/C)=199.00099(Гц);
Теперь необходимо определиться с временами. Преждте всего это время полета до цели - Т1=142492 с по собственным часам А. Все это время будет приниматься частота f1. А что будет сразу после разворота? Вот тут и наступает новый момент! Дело в том, что сразу после разворота А оказывается в одной инерциальной системе с волновым порядком, расходящимся от Б! Мне могут возразить, что в это же время развернулся и Б. Не вдаваясь в обсуждение вопроса, что такое "в это же время ", отвечу, что А не может узнать о факте разворота Б раньше, чем встретит фронт изменения волнового порядка, возникший при его развороте! А до этого момента А движется в волновом порядке Б так, как будто А и Б взаимно неподвижны. И частота, которую принимает А, f0=1(Гц).
Остается найти время Т0 и Т2. Это можно сделать по разному. Например, вернуться в ИС центра разлета и рассмотреть задачу о встрече волнового фронта от события разворта Б и возвращающейся ракеты А. Так и поступим:
T'*V+T'*C=2L; T'=2L/(V+C);
T'=2000000/(1+0.99)=1005025.125
для перехода к времени ракеты А разделим это время на Г0: (Г0 - из прошлой задачи, ведь мы сейчас в ИС Земли!)
Т0=Т'/G=1005025.125/7.08881=141776. 28 c.
Ну и время, в течение которого будет приниматься сигнал на повышенной частоте - то что останется от времени возвращения после вычета времени до встречи волнового фронта, несущего информацию о развороте ракеты Б:
Т''=L/V-2L/(V+C)= (L/V)*((C-V)/(C +V))=1000000*0.01/(0.99*1.99)=5 075.884 c ,
или по часам А:
T2=T''/G=5075.884/7.08881=716.0 4 c
Наконкц, общая проверка:
N=f1*T1+f0*T0+f2*T2=142492.3*0.0050251+1 41776.28 *1+716.04*199.00099=
=716.04+141776.28 +142492.3=284984.6,
или тех же 284984 секунды!
Таким образом, несмотря на существенно изменившиеся условия измерений, каждый из близнецов определит длительность полета другого в полном соответствии с его (другого) собственными часами.

 Рис. 2.

   На Рис.2 представлен график приема частот одним из близнецов при симметричном полете. Для сохранения ноглядности, масштабы не собдюдены.

   Таким образом, уравнения СТО при их последовательном использовании показывают полное отсутствие каких либо "парадоксов". Более того, решенные задачи в числах демонстрируют удивительную точность и самосогласованность СТО!

     И в завершение - об ускорении. Да, бесконечное ускорение невозможно. Но это и не нужно! Важно только, чтобы период ускорения-замедления занимал достаточно малое время в графике движения ракеты. Тогда его вклад будет малым, а практически вся разность времени будет накоплена именно на участках инерциального движения...