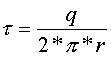
На главную страницу | Мои темы
Заряженное кольцо
А я вот все перерыл - и ни черта не могу найти формулу для электростатического поля в любой точке плоскости заряженного (равномерно хотя бы) кольца.
Таков был вопрост одного из участников форума на Мембране. Попробуем получить искомую формулу...
Пусть имеется: кольцо радиуса r, Заряженное с линейной плотностью заряда
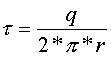
Найдем напряженность, создаваемую кольцом в точке, отстоящей на R от центра кольца в плоскости кольца (Рис. 1).
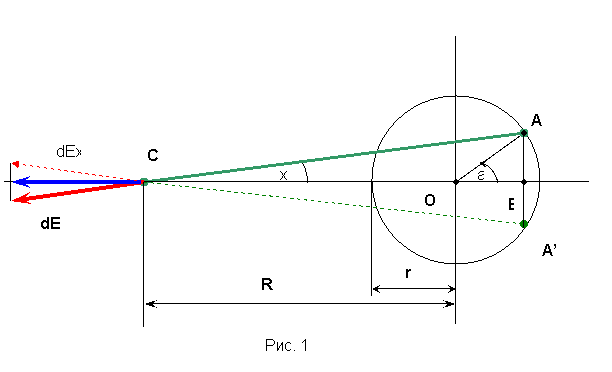
Для решения выберем элементарный участок дуги кольца dа (точка А). На нем содержится заряд
![]() (1);
(1);
Этот заряд создает в точке C элементарный вектор напряженности dE.
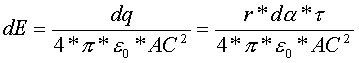 (2);
(2);
Найдем расстояние от участка кольца до точки. Для этого используем тр. OAC и теорему косинусов:
![]() (3);
(3);
Теперь обратим внимание на наличие симметричной точки A’ и на то, что создаваемый этой точкой вектор также равен по модудю и направлен симметрично оси х. Поэтому проекции векторов на ось «y» компенсируются, а прекции на ось «x» - удваиваются. Поэтому элементарный вектор напряженности, создаваемый ДВУМЯ симметричными элементами кольца,
удваивается:
![]() (4);
(4);
Остается определить cos(x). Это легко сделать из рассмотрения тр. ABC:
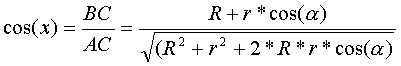 (5);
(5);
Окончательно значение проекции элементарного вектора напряженности будет иметь вид:
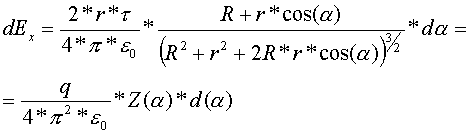 (6);
(6);
Для нахождения ПОЛНОГО значения вектора напряженности в точке С,
необходимо проинтегрировать выражение (6) по углу а в преднлпх от «0»
до Pi. При этом будут учтены ВСЕ заряды, находящиеся на кольце:
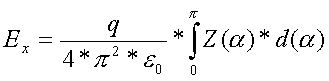 (7);
(7);
И вот тут возникает проблема. Ниже приводятся результаты интегрирования для функции Z(a).

Вот и вылезли эллиптические интегралы! А вот их расшифровка:

А главная проблема в том, что эллиптические интегралы несводимы к обычным функциям. Таким образом, ценность найденного решения, на мой взгляд, невелика.
Конечно, если вычислитель умеет обращаться с такими функциями, это может помочь в расчетах. Но я лично прдпочел бы воспользоваться одним из бесчисленных приемов числового интегрирования выражения для Z(a).
При разумном числе разбиений процедура не займет много времени.
...Теперь понятно, почему нигде нет стандартной формулы расчета параметров поля вокруг заряженного кольца? Мне – да.
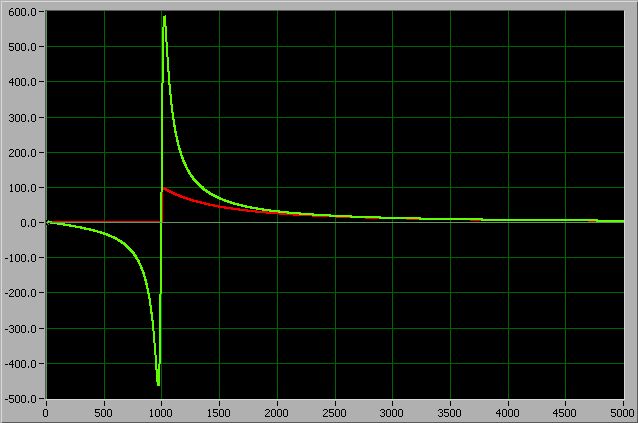
Рис. 2.
На Рис. 2 представлен график напряженности как функция расстояния от произвольной точки до центра заряженного кольца. Радиус кольца составляет 1000 ед. Красная линия представляет график напряженности, создаваемой заряженной тем же зарядом сферой. При удалении от кольца графики быстро сближаются. На первый взгляд может показаться, что в точке, соответствующей радиусу кольца, функция терпит разрыв. Но это не так.
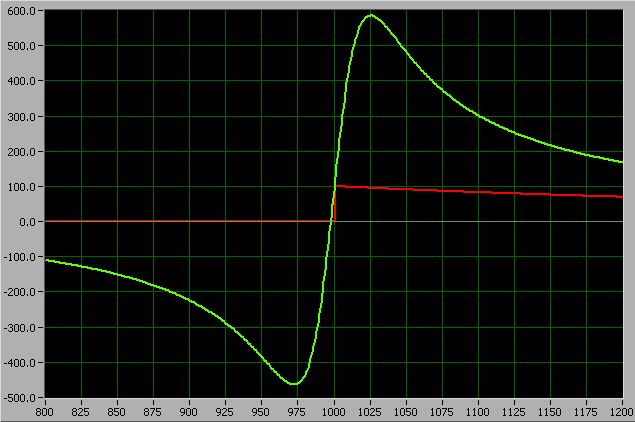
Рис. 3
На Рис. 3 представлен график функции в непосредственной близости от кольца.
На самом кольце напряженность поля в точности соответствует напряженности от заряженной проводящей сферы!
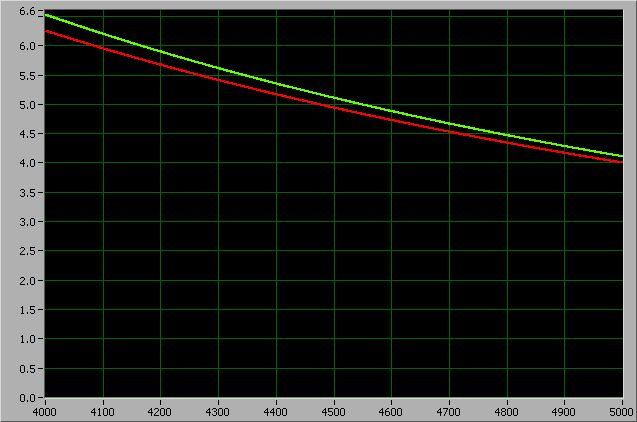
Рис. 4
На рис. 4. представлен график функций вблизи отметки R=5*r. Видно, насколько график искомой функции сблизился с графиком напряженности поля заряженнрой сферы...